http://web.stanford.edu/class/cs224w/
CS224W | Home
Content What is this course about? Complex data can be represented as a graph of relationships between objects. Such networks are a fundamental tool for modeling social, technological, and biological systems. This course focuses on the computational, algor
web.stanford.edu
본 포스팅은 CSS224W 강의를 들으며 필요한 내용을 요약한 것이다. 필자 주관적으로 필요한 부분만 요약되어 있으니, 참고하길 바람.
2. Traditional Methods for ML on Graphs
1) Node Features
ML에 Graph 자료구조를 활용하기 위한 내용들을 살펴본다. 먼저 Node-Level Features를 만들기 위한 방법을 살펴볼 것이다. 노드에서 사용 가능한 피쳐들은 다음과 같이 정의할 수 있다. 각각의 피쳐를 만드는 방법은 생략하도록 한다. (강의내용 참고)
- Node degree
- Node centrality
- Clustering coefficient
- Graphlets
정리하자면 크게 두 가지 방법으로 Node의 features를 벡터 형태로 표현하는 것인데, Importance-based features, 그리고 Structure-based features 두 가지 방법이 그것이다. Importance-based의 첫 번째는 Node degree로, 단순 count 가중치 표현을 한 것이고, 두 번째는 Node Centrality로 eigenvector, betweenness, closeness centrality로 표현한 것이다. 이러한 표현 방법은 그래프 내에서 가장 Influential 한 노드를 predict 하는 데 유용한 피처로 사용될 수 있다.
그리고 Structure-based 방법은 Node degree, clustering coefficient, graphlet degree vector 표현 방법이 있는데, 특정 노드가 어떤 기능적 역할을 하는지(classification인 듯 하다) 정하는 것에 유용하다.
2) Link prediction
그래프 내의 노드들이 다음에는 어떤 link로 연결이 강화될 지를 예측하는 Link prediction에 대한 내용이다. 노드간의 Link prediction은 크게 두 가지 방법론으로 formulate 할 수 있다.
- Links missing at random
- Links over time

두 가지 중에 어떤 방법을 쓰던, 학습을 하는 Methodology는 다음과 같다. 우선 예측이 되는 대상, pair of nodes (x,y)를 선정하고 각 쌍에 대해 prediction score c(x, y)를 계산한다. 그리고 스코어 순으로 각 쌍을 정렬한 뒤, Ground truth(랜덤 제거 전 혹은 특정 시간 이후)와 얼마나 다른지 비교한다.
그리고 prediction에 사용하는 Link-Level Features는 다음과 같다.
[Distance-based feature]
Shortest-path between two nodes와 같은 피쳐를 생성할 수 있다.
[Local neighborhood overlap]
두 노드간에 shared 된 영역에 대해 count, 자카드 계수 계산, Admic-Adar 계수 계산 등으로 집합관계를 수식으로 표현하는 방법의 피쳐를 생성할 수 있다. 그러나 서로 접하지 않는 노드간에는 아무런 정보도 없다는 한계점을 가지고 있다.
[Global neighborhood overlap]
Katz index 라는 것은 local neighborhood overlap의 단점을 보완하는 방법으로, 주어진 그래프 내의 edge를 모두 활용 하는 것이다. 그래서 서로 접하지 않아도 대부분의 노드쌍 u,v 의 관계를 활용할 수 있다. 대략적인 아이디어는 A_{uv}^{k} 라는 "#paths of length k between node u, v" 정보를 계산한다. 조금 더 쉬운 말로 하면, 길이가 k인 u, v 사이의 경로 갯수를 count 한다는 것이다. 그리고 이 정보를 모든 k, 즉 1부터 infinite까지 더하여 아래와 같은 수식을 정의한다.
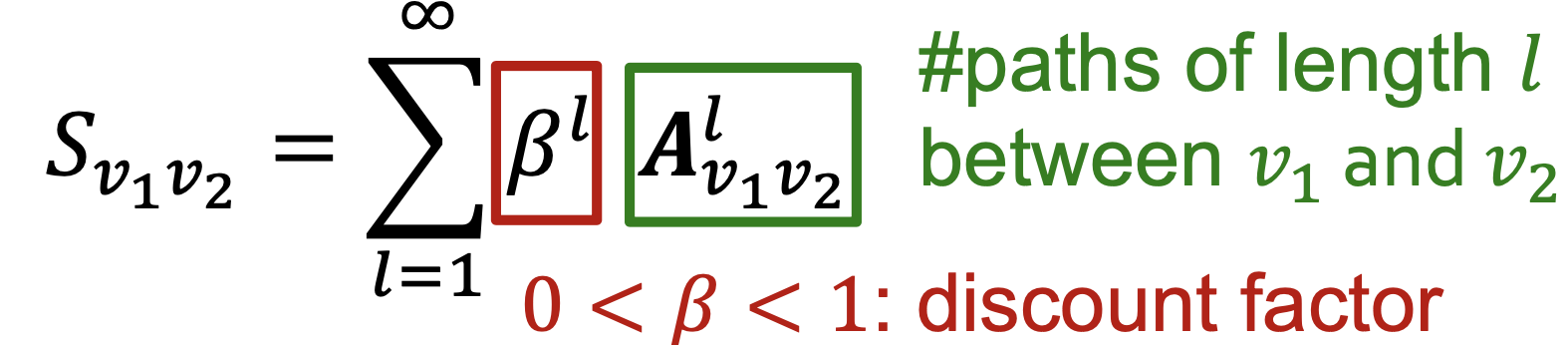
이를 효율적으로 계산 하기 위해 adjacency matrix를 활용한다. 수식을 전개하다보면 adjacency matrix 요소의 곱이 더해지는 각 element 라는 것을 발견할 수 있는데, 이 때문에 매우 쉽게 계산이 가능하다. graph 자료구조에서 adjacency matrix가 얼마나 유용한지를 다시 한 번 강조할 수 있는 대목이다.
3) Graph structure representation
node와 edge를 벡터 형태로 표현하는 것 외에, 그래프 구조 자체를 representation 하는 경우도 존재한다. 그래프 표현은 위에서 소개한 표현들에서 크게 벗어나지 않으며, 주로 그래프간의 Similarity를 계산하기 위한 Kernel로 디자인된다. 아래는 그래프 표현 방법들이며, 자세한 내용은 역시나 생략한다.
- Graphlet Kernel
- Weisfeiler-Lehman Kernel
'Programming & Machine Learning > CS224W 강의요약' 카테고리의 다른 글
| [CS224W: Machine Learning with Graphs 강의 내용 요약 - 1] (0) | 2021.06.01 |
|---|
