행렬 분해와 차원 축소의 기법들 - [2]
지난 포스팅에서는 PCA, SVD를 위주로 한 행렬 분해 기법들에 대해 다루었고, 이어서 행렬 분해와 차원 축소의 기법들을 마저 알아보자. 본 포스팅에서는 확률적 차원축소 방법 중 가장 대표적인 알고리즘인 t-SNE, 그리고 행렬 분해를 기반으로 한 Matrix Factorization과 ALS(Alternating Least Squares)에 대해 서술하겠다. MF와 ALS의 경우 차원 축소에서 언급하기엔 조금 애매한 감이 있지만, 근본적으로 Latent factor를 분석하는 것과 차원 축소의 분석 방법이 크게 다르지 않기 때문에 이번 포스팅에 포함시켰다.
1. t-SNE를 이용한 차원 축소
머신 러닝에 대한 접근법은 전통적인 관점에서 두 가지로 나뉜다. 첫 번째는 행렬과 미분 등을 이용한 최적화로 문제에 접근하는 방법, 그리고 두 번째는 확률적 관점에서 likelihood를 maximize 하거나 distribution의 관점에서 문제를 풀어나가는 방법이다. t-SNE는 두 번째 방법으로 차원 축소라는 Machine Learning 문제를 해결하는 가장 대표적인 방법 중 하나이다. 주로 자연어처리에서 임베딩 방법 중의 하나로 많이 사용되었고, 차원 축소보다는 시각화의 용도로 더 많이 사용되기도 하는 알고리즘이다. 또한 통계학적으로 매우 탄탄한 이론에 기반하기 때문에, 전체 과정을 완전히 이해하고 따라가는 것은 쉽지 않지만, 동작 원리 자체를 intuitive하게 이해하는 것은 그리 어렵지 않다.
필자는 개인적으로 t-SNE와 같이 확률론적 관점에서 이러한 문제를 푸는 것을 선호하는 편인데, 실제 데이터를 분석하다보면 특정한 분포를 가정하여 문제를 푸는 것이 훨씬 효과적이었던 얕은 경험을 가지고 있기 때문이다(실제 데이터는 Skewness 문제 때문에 이런 상황이 매우 빈번하게 발생한다). 또한 명확한 정답이 없는 문제를 풀 때에는 시각화라는 것이 매우 강력한 무기가 된다.
이제 t-SNE에 대해 요약하면, t-SNE는 특정 분포를 가정하여(가우시안 분포, t-분포) 데이터의 지점간의 관계를 모델링한 알고리즘으로, 데이터 Xi와 Xj의 등장 관계를 확률적으로 표현하는 것이다. 그래서 먼저 원 데이터 X의 데이터 지점간의 관계를 아래의 식과 같이 확률적으로 표현한다. 이를 Stochastic Neighbor Embedding, 즉 SNE라고 한다.

그리고 다음으로, 차원 축소한 뒤의 데이터를 X`라고 할 때, 축소된 데이터 지점간의 관계 역시 모델링한다. 단, 연구 결과에 따르면 X`는 가우시안 분포를 가정하는 것 보다 t-분포를 가정하는 것이 훨씬 좋은 결과를 냈기 때문에 X`의 확률 q는 t-분포를 따르게 한다. 그래서 t-SNE라고 불리는 것이다.
그러면 이제 여기서 두 개의 확률 분포를 얻어낼 수 있다. 그리고 이 확률 분포의 분산을 최소화 하면, 훌륭하게 차원 축소를 수행했다는 결론에 도달할 수 있다. 그래서 Cost function으로 당연하게도 KL-Divergence를 사용하며 이를 Gradient Descent 같은 최적화 문제로 풀게 된다. 식으로는 아래와 같다.

여기까지 t-SNE를 intuitive하게 설명했다. 패키지 레벨에서 사용하는 방법과 코드는 (이곳)을 참고하면 된다.
2. Matrix Factorization
1) Latent Factor
MF에 대한 자세한 설명은 (링크)를 참고하도록 하고, 본 포스팅에서는 ALS를 이해하기 위한 Basic concept와 equation만 알아보자. MF는 추천 시스템에서 흔히 사용되는 Latent Factor Model이다. Latent Factor라는 것 역시 본질적으로는 SVD와 같이 원래의 Matrix에서 행과 열에 해당하는 요소들을 각각의 관점에서 k개로 축소시켜 벡터로 표현한다는 것이기 때문에, 차원 축소와 일맥 상통한다고 할 수 있다. 거두절미하고 아래와 같은 그림이 있을 때, 행은 유저(U), 열은 아이템(I), 그리고 요소 값은 점수(Rating) 이라고 하자.

그러면 아래와 같은 두 식으로 다시 표현할 수 있고, 여기에서 P와 Q는 각각의 Latent factor가 된다. 위에서도 언급했지만, 이러한 모양은 SVD를 활용한 행렬 분해와 같은 개념이라고 볼 수 있다.
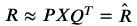

2) Cost Function & Train
MF의 Cost function은 rating 값을 기준으로 한 MSE가 가장 일반적이다. L2 Regularization을 적용한 MF의 Cost function은 다음과 같다.

이제 이 Cost function을 활용하여 Latent Factor를 찾기 위한 최적화를 수행해야 하는데, 여기서 일반적인 최적화 방식인 Gradient Descent, 그리고 ALS을 나눠서 설명하도록 하겠다. 먼저 GD에 대해 살펴보자. GD를 수행하기 위해서는 q와 p에 대해 모두 편미분을 수행하여, 다음과 같이 각각에 대한 gradient를 한번에 구한 뒤 계수를 업데이트하는 방식이다.

3) Alternating Least Squares
ALS는 Gradient Descent와 다르게, 각각의 Latent Factor를 Alternately하게 학습하는 방법이다. Alternately하게 학습한다는 것은 하나의 Latent Factor X를 학습할 때, 다른 Latent Factor Y를 상수로 간주하여 계산한 뒤 X를 먼저 업데이트 하고, 연이어서 같은 방법으로 Y를 업데이트 하는 것을 의미한다. 즉, Latent Factor가 서로 독립적으로 학습을 수행하는데, 서로를 상수로 간주하여 순차적으로 Alternately Training을 한다는 것이다. 서로를 상수로 간주하게 되면, Gradient Descent와 달리, Deterministic하게 학습이 가능하게 된다. 아래의 식은 Alternately한 과정에서 X의 관점이다. C와 p는 MF에서 조금 더 추가된 개념인데, 없는 계수라고 생각하고 식을 이해해도 무방하다. 자세한 내용은 논문을 참조하는 것이 좋다.

그리고 ALS에 대한 간단한 구현 코드는 아래와 같다. 만약 수식에 대해 조금 더 이해하고 싶다면 (링크)를 참고하자.
import numpy as np
class ALS:
def __init__(self, R, k, r_lambda, confidence, epochs, verbose=False):
"""
:param R: rating matrix
:param k: latent parameter
:param r_lambda: alpha on ALS
:param confidence: confidence on ALS
:param epochs: training epochs
:param verbose: print status
"""
self._R = R
self._num_users, self._num_items = R.shape
self._k = k
self._r_lambda = r_lambda
self._confidence = confidence
self._epochs = epochs
self._verbose = verbose
self._init_vectors()
def _init_vectors(self):
# init latent features
self._U = np.random.normal(size=(self._num_users, self._k))
self._I = np.random.normal(size=(self._num_items, self._k))
# make binary rating matrix P
self._P = np.copy(self._R)
self._P[self._P > 0] = 1
# make confidence matrix C
self._C = 1 + self._confidence * self._R
def fit(self):
"""
fit ALS model
"""
# train while epochs
self._training_process = []
for epoch in range(self._epochs):
self.alternating_least_squares()
cost = self.cost()
self._training_process.append((epoch, cost))
# print status
if self._verbose == True and ((epoch + 1) % 10 == 0):
print("Iteration: %d ; cost = %.4f" % (epoch + 1, cost))
def cost(self):
"""
compute root mean square error
:return: rmse cost
"""
r_hat = self.predict()
confidence_loss = np.sum(np.power(self._C * (self._P - r_hat), 2))
regularization_term = self._r_lambda * (np.sum(np.power(self._U, 2)) + np.sum(np.power(self._I, 2)))
return np.sqrt(confidence_loss + regularization_term)
def alternating_least_squares(self):
"""
ALS optimizer
"""
# update_y_u
for u in range(self._U.shape[0]):
C_u = np.diag(self._C[u])
left_equation = self._I.T.dot(C_u).dot(self._I) + np.dot(self._r_lambda, np.identity(self._U.shape[1]))
right_equation = self._I.T.dot(C_u).dot(self._P[u])
self._U[u] = np.linalg.inv(left_equation).dot(right_equation)
# update x_i
for i in range(self._I.shape[0]):
C_i = np.diag(self._C[:, i])
left_equation = self._U.T.dot(C_i).dot(self._U) + np.dot(self._r_lambda, np.identity(self._I.shape[1]))
right_equation = self._U.T.dot(C_i).dot(self._P[:, i])
self._I[i] = np.linalg.inv(left_equation).dot(right_equation)
def predict(self):
"""
calc complete matrix U X I
"""
return self._U.dot(self._I.T)
def print_results(self):
"""
print fit results
"""
print("Final RMSE:")
print(self._training_process[self._epochs-1][1])
print("Final R matrix:")
for row in self.predict():
print(["{0:0.2f}".format(i) for i in row])
# run example
if __name__ == "__main__":
# rating matrix - User X Item : (7 X 5)
R = np.array([
[1, 0, 0, 0, 3],
[2, 0, 0, 1, 0],
[0, 2, 0, 5, 0],
[1, 0, 0, 0, 4],
[0, 0, 5, 4, 0],
[0, 1, 0, 4, 0],
[0, 0, 0, 1, 0],
])
# P, Q is (7 X k), (k X 5) matrix
factorizer = ALS(R, k=8, r_lambda=40, confidence=40, epochs=50, verbose=True)
factorizer.fit()
factorizer.print_results()
참고 자료들
- http://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
- https://ratsgo.github.io/machine%20learning/2017/04/28/tSNE/
- https://yamalab.tistory.com/92
- http://yifanhu.net/PUB/cf.pdf
- https://yeomko.tistory.com/4
- https://datascienceschool.net/view-notebook/fcd3550f11ac4537acec8d18136f2066/