본 포스팅은 Factorization Machine의 intuitive한 설명(블로그 번역 + 필자 개인적 해석)과 라이브러리 활용법에 대한 포스팅의 후속이다. FM이 sparse한 피처간의 pair-wise interaction을 학습한다는 것을 어렴풋이 이해했다면, 이번에는 실제로 Science 레벨에서 모델링 할때 어떻게 활용해야 하는지를 수식 레벨부터 직접 코드로 구현해보면서 따라가보자. 백문이 불여일견이라 하였으니, 코드 역시 마찬가지일 것이다.
이번 글에서는 FM의 intuitive한 설명은 생략하고 실제로 벡터 단위로 어떤 분석을 수행해야 하는지, pair-wise한 학습을 하면 어떤 이득을 얻을 수 있는지에 대해서 중점적으로 서술하였다.
1. Algorithm Concept
intuitive한 설명은 생략한다고 하였지만, 알고리즘의 철학 정도는 다시 짚고가는 것이 좋겠다. FM이라는 알고리즘의 개요는 다음과 같다.
Factorization Machine은 SVM처럼 동작하는 General predictor이다. 이 알고리즘의 Edge point는 변수 간의 모든 pair-wise interaction을 계산한다는 것이다. 이렇게 함으로써 얻을 수 있는 가장 큰 이득은 아주 sparse한 데이터셋을 가지고 'cold-start'를 극복 할 수 있다는 것. 얼핏 보면 마치 latent vector처럼 동작하는 것 같지만, interaction 자체를 factorized feature로 활용한다는 것이 다르다. 따라서 이 알고리즘은 SVM과 같은 알고리즘이 가지는 좋은 성능의 prediction, 그리고 SVD++ 같은 알고리즘이 가지는 숨겨진 의미 단위(latent vector) 해석의 장점을 모두 가지고 있으며, 동시에 sparse한 데이터셋에서도 길을 잃어버리지 않게 설계된 알고리즘이라고 할 수 있다.
FM의 후속 연구로는 이를 응용하여 더 발전된 구조를 가진 FFM, AFM, PNN 등의 연구가 있다. 따라서 현재 SOTA는 아니지만, 기본적으로 SVM이나 SVD++ 처럼 성능과 철학이 검증된 predictor라고 볼 수 있다. 또한 wide and deep과 함께 feature를 factorizing(Conjunction)하여 사용하는 알고리즘 계열의 baseline이라고 볼 수 있다. 이를 추천 시스템의 관점에서 보면, implicit 데이터를 이용해 candidate를 생성하는 역할을 주로 Association Rule, SVD++, kNN 같은 알고리즘이 수행하고, feature factorizing을 통한 re-rank 역할은 FM 같은 알고리즘이 수행한다고 볼 수 있다.
또한 C, JAVA, Python등의 언어를 활용할 수 있고 ALS이나 Adagrad optimizer를 사용할 수 있는 오픈 소스도 몇 개 개발되어 있다. (다만, docker같은 환경에서는 production 레벨의 사용성이 그닥 좋지는 않다..)
2. Equation 구현
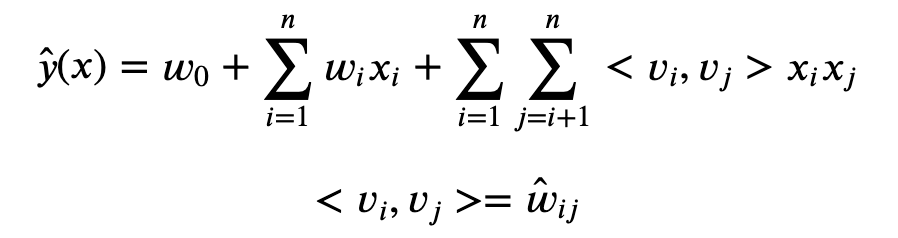
위의 식처럼 모델의 equation은 아주 간단하다. 단, 세 번째 항을 보면 inference 시에 O(n^2)가 된다는 것을 알 수 있다. 그래서 계산 복잡도를 줄여주는 과정이 필요한데, 아래의 수식처럼 전개하면 O(kn)이 된다. Numpy로 계산하면 densed feature만 계산하기 때문에 실제로는 더 낮은 복잡도를 가진다. 전개 과정이 그리 어렵지 않으니 직접 손으로 따라서 써보자.
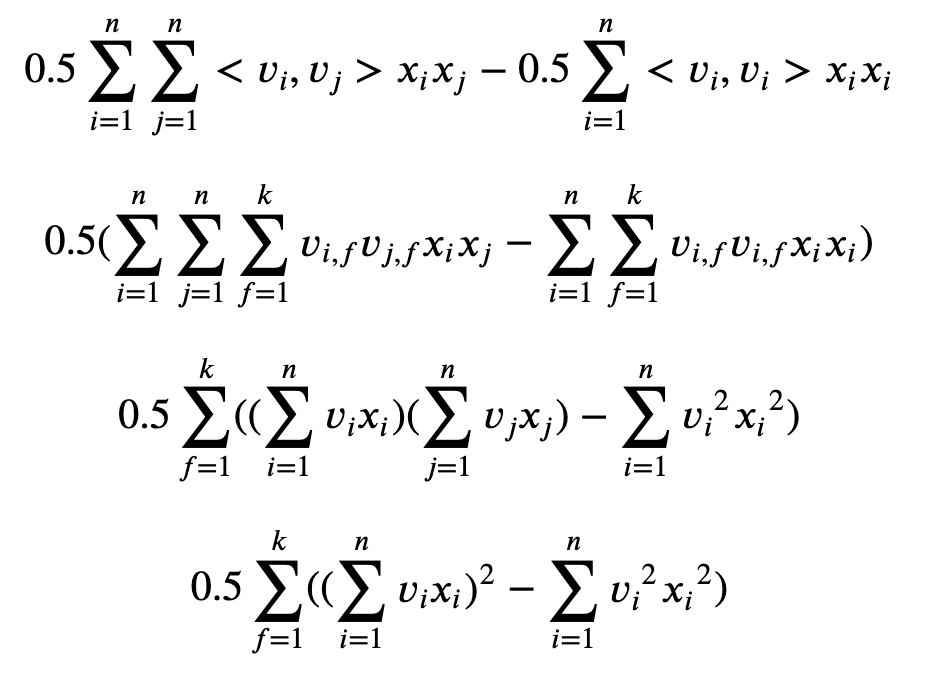
전개 과정에서 한가지 생략된 것은 첫 항을 만들어내는 것이다. 그래서 이 항이 어떻게 생겨났냐? 라는 질문이 생길 수도 있다. 그럴 땐 equation의 세번째 항을 사각형의 2D Matrix로 그려보면 직관적으로 이해할 수 있다. 이 전개 방법이 어떤 이름의 공식에서 파생된 것인지는 잘 모르겠다(필자는 수학/통계학 관련해서는 비전공자에 가깝기 때문에 수학적 지식이 다소 없는 편이라 죄송하다). 그냥 직관적으로 받아들였다.
아무튼 이 수식을 그대로 파이썬 코드로 옮겨보자. 이미 학습을 통해 b, w, v 벡터들을 모두 구한 뒤라고 가정하겠다. x 피처의 개수가 4개, v 피처의 k 파라미터를 4라고 하였을 때 아래와 같이 표현할 수 있다.
import numpy as np
# Pre-trained parameters
b = 0.3
w = np.array([0.001, 0.02, 0.009, -0.001])
v = np.array([[0.00516, 0.0212581, 0.150338, 0.22903],
[0.241989, 0.0474224, 0.128744, 0.0995021],
[0.0657265, 0.1858, 0.0223, 0.140097],
[0.145557, 0.202392, 0.14798, 0.127928]])
# Equation of FM model
def inference(data):
num_data = len(data)
scores = np.zeros(num_data)
for n in range(num_data):
feat_idx = data[n][0]
val = np.array(data[n][1])
# linear feature score
linear_feature_score = np.sum(w[feat_idx] * val)
# factorized feature score
vx = v[feat_idx] * (val.reshape(-1, 1))
cross_sum = np.sum(vx, axis=0)
square_sum = np.sum(vx*vx, axis=0)
cross_feature_score = 0.5 * np.sum(np.square(cross_sum) - square_sum)
# Model's equation
scores[n] = b + linear_feature_score + cross_feature_score
# Sigmoid transformation for binary classification
scores = 1.0 / (1.0 + np.exp(-scores))
return scores
# Inference test for 3 case
data = [[[0, 1, 3], # feature index
[0.33, 1, 1]], # feature value
[[2],
[1]],
[[0, 1, 2, 3],
[0.96, 1, 1, 1]]]
inference(data)보통 sparse한 데이터를 표현할 때 libsvm format(<label> <index1>:<value1> <index2>:<value2> ...) 이라고 불리는 포맷을 사용하기 때문에, 코드에서는 이를 조금 더 쉽게 사용하기 위해 ([index list], [value list])를 element로 하는 list를 데이터셋으로 사용하였다.
3. Training 구현
본 포스팅에서는 regressor 대신, SGD를 포함한 binary classifier를 구현체로 사용한다. 만약 regressor를 직접 구현해보고 싶다면, sigmoid 과정을 제거하고 SGD에 사용하는 편미분 식만 변경하면 된다. binary classifier 구현 과정은 다음과 같다.
1) equation 결과에 sigmoid 함수를 씌워준다. (return : z)
2) cost function은 equation을 z로 하는 cross-entropy를 사용한다.
3) Theta의 업데이트는 아래의 수식처럼 b, w, v 단위로 편미분하여 Gradient Descent를 수행한다. 일반적인 binary classification에 사용하는 Gradient Descent 수식에 Gradient만 변수의 type(global bias b, linear coef w, factorized coef v)별로 다르게 적용한다.
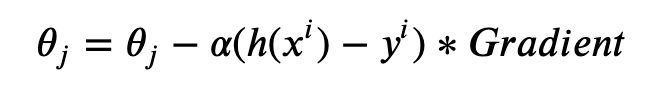
b와 w의 편미분은 아주 간단한 식으로 나타낼 수 있지만, v는 계산이 아주 조금 복잡하다(물론 linear time에 계산된다). 아래의 수식은 변수의 타입별로 편미분한 결과이다. 이 역시 어렵지 않으니 손으로 직접 편미분을 전개해보는 것을 추천한다.

위 수식들을 기반으로 Cost Function과 Stochastic Gradient Descent를 구현한 코드는 아래와 같다. 필자의 경우 L2 정규화를 각 변수 타입마다 추가해주었는데, 모델의 철학을 처음 이해했을 때에는 L2 정규화가 크게 효과가 있을 것 같지 않다는 멍청한 생각을 했었다. (어차피 pair-wise 하게 완전히 독립성이 보장된 상태로 학습을 할 텐데, 굳이 L2 정규화로 피처를 눌러주는 작업이 필요한가?) 하지만 실제 extreme sparse dataset으로 모델링을 해보면, L2 정규화를 적용하는 것이 과적합을 꽤나 잘 방지한다는 것을 알 수 있다. (사실은 독립성을 보장하는 형태로 학습하는 게 아니고, 정확히 그 반대이기 때문이다. pair-wise interaction을 통해 모든 피처간의 숨겨진 연관성을 학습할 수 있는 것이다. 그래서 cold-start를 극복하는 것에도 도움을 준다는 것.)
def _get_loss(self, y_data, y_hat):
"""
Calculate loss with L2 regularization (two type of coeficient - w,v)
"""
l2_norm = 0
if self._l2_reg:
w_norm = np.sqrt(np.sum(np.square(self.w)))
v_norm = np.sqrt(np.sum(np.square(self.v)))
l2_norm = self._l2_lambda * (w_norm + v_norm)
return -1 * np.sum( (y_data * np.log(y_hat)) + ((1 - y_data) * np.log(1 - y_hat)) ) + l2_norm
def _stochastic_gradient_descent(self, x_data, y_data):
"""
Update each coefs (w, v) by Gradient Descent
"""
for data, y in zip(x_data, y_data):
feat_idx = data[0]
val = data[1]
vx = self.v[feat_idx] * (val.reshape(-1, 1))
# linear feature score
linear_feature_score = np.sum(self.w[feat_idx] * val)
# factorized feature score
vx = self.v[feat_idx] * (val.reshape(-1, 1))
cross_sum = np.sum(vx, axis=0)
square_sum = np.sum(vx * vx, axis=0)
cross_feature_score = 0.5 * np.sum(np.square(cross_sum) - square_sum)
# Model's equation
score = linear_feature_score + cross_feature_score
y_hat = 1.0 / (1.0 + np.exp(-score))
cost = y_hat - y
if self._l2_reg:
self.w[feat_idx] = self.w[feat_idx] - cost * self._lr * (val + self._l2_lambda * self.w[feat_idx])
self.v[feat_idx] = self.v[feat_idx] - cost * self._lr * ((sum(vx) * (val.reshape(-1, 1)) - (vx * (val.reshape(-1, 1)))) + self._l2_lambda * self.v[feat_idx])
else:
self.w[feat_idx] = self.w[feat_idx] - cost * self._lr * val
self.v[feat_idx] = self.v[feat_idx] - cost * self._lr * (sum(vx) * (val.reshape(-1, 1)) - (vx * (val.reshape(-1, 1))))
4. 전체 구현 코드
지금까지 Equation과 Training을 위주로 수식과 코드를 살펴보았다. 이를 하나의 Class로 엮어 간단한 Example로 구현해놓은 코드는 github을 참고하면 된다. (논문을 보고 간단히 공부용으로 구현한 것이기 때문에, Cython을 활용하거나 병렬처리를 해주거나 하는 production 레벨의 코드는 없다) 참고로, 해당 repo에는 타이타닉 데이터셋을 libsvm format으로 변경해둔 데이터셋을 함께 넣어두었다. FM.py 파일을 실행하기만 하면 된다.
전체 구현 코드는 high level에서는 다음과 같은 수식들을 따른다고 볼 수 있다.

5. w, v 벡터에 대한 분석
먼저 V 벡터의 동작 원리에 대해 생각해보자.
일반적인 Matrix Factorization에서는 W = V ' Vt 를 만족하기 위해, k를 충분히 크게만 하면 어느정도의 성능이 보장됐다(Overfit은 또 다른 문제이지만). Factorization Machine 역시 마찬가지의 메커니즘(Factorization)을 기반으로 동작하기 때문에, k가 클수록 V를 잘 표현할 수 있다고 생각할 수도 있다. 하지만 FM은 조금 다른 것이, k가 어느 정도 작게 선택되어야 더 성능이 좋다는 것이다. 왜냐면 FM이 가정하는 R^n은 매우 sparse 하기 때문이다. k가 늘어날수록 Equation에 사용하는 파라미터가 기하급수적으로 증가하는데, 이 때문에 차원의 저주에 빠진 것 같은 효과가 날 수 있다. 따라서 k를 적당히 작게 설정했을 때가 성능이 가장 좋다.
그렇다면 MF보다 FM이 더 효과적인 이유는 무엇일까? 그 이유는 parameter를 factorizing 함으로써 MF의 한계인 피처간 독립성 문제를 극복할 수 있기 때문이다. 이 말인 즉슨, MF 기반의 Factorizing은 두 변수간의 독립적인 관계만 학습을 하지만, FM은 변수끼리 pair-wise 하게 학습하기 때문에 하나의 변수가 또 다른 다른 변수의 학습에 영향을 줄 수 있게 된다는 것이다. 이게 k를 어느 정도 작게 설정해야 하는 이유가 되기도 하며 앞서 말한 L2 정규화를 해야 하는 이유이다. 결론적으로 FM이 MF처럼 k 파라미터를 사용하는 것은 Factorization 기반의 알고리즘의 한계를 극복하는 것을 의미한다. MF, SVD 같은 알고리즘은 제한된 상황의 데이터셋(u,i,r)을 사용하기 때문에, 다양한 피처를 활용하기에 힘들다. 반면 FM은 implicit한 요소만 추출해내는 것이 아니라, 사용 가능한 모든 피처 단위의 interaction을 계산하기 때문에 meta-data를 활용하려는 상황에서 큰 장점을 가진다.
그렇다면, 하나의 피처가 pair-wise interaction을 통해 모델에 영향을 미치는 것에 대한 분석이 매우 중요해진다. w는 linear regression의 coef와 유사한 역할을 하지만, v는 마치 비선실세(?) 같은 역할을 하기 때문이다. 이 역시 Titanic 데이터셋을 통해 간단히 알아보도록 하자. 아래의 그래프는 Titanic 데이터셋의 피처를 모두 더미 인코딩한 뒤 v 벡터의 해당하는 값을 모두 더해(k=1~4), 간단하게 영향력을 살펴본 것이다.

이를 해석하면, coef가 양수로 나온 피처는 전반적으로 binary classification에 긍정적인 feature interaction을 제공했다고 생각할 수 있고, 반대로 음수라면 부정적인 feature interaction을 제공했다고 생각할 수 있다. 하지만 긍/부정이 아니라 더 정확한 영향을 알아보려면 절대값들을 더한 뒤 관찰하는 것이 좋다. 아래의 그래프는 v 벡터를 절대값으로 변환한 뒤, 같은 x_i 내에서의 값들을 모두 더한 것을 피처 단위로 나타낸 것이다.
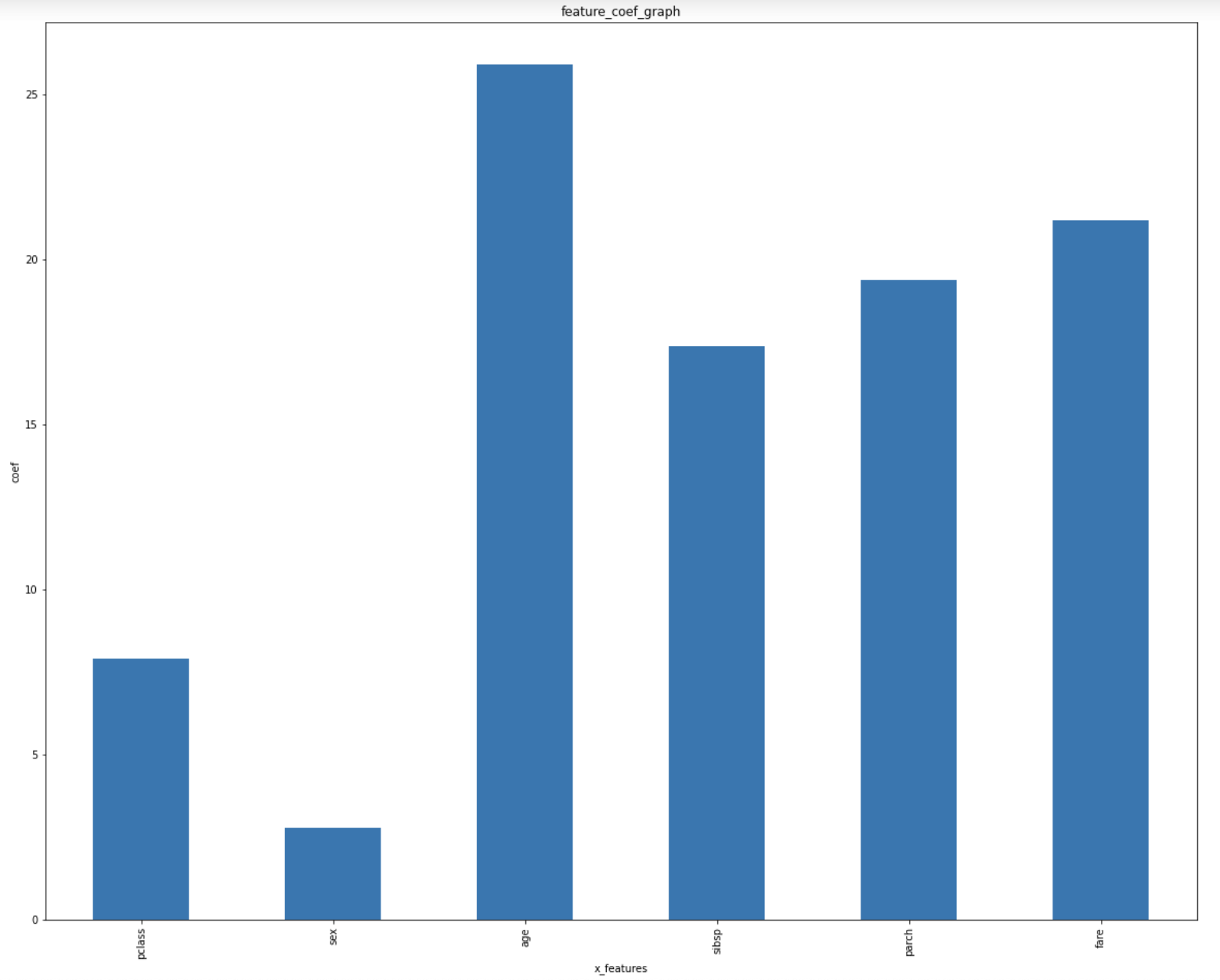
말로 설명하니 다소 장황한데, 코드를 보는 것이 훨씬 이해가 빠르다. 쉬운 이해를 돕기 위해 주피터 노트북으로 작성해 두었다. (github) 결론만 말하자면, 피처 단위로 분석하는 것은 총 3가지 정도를 수행할 수 있다. 해결하려는 문제의 상황에 맞게 선택하는 것이 좋겠다.
1) w 벡터의 coef 분석 : 전체적인 영향력을 볼 수 있다.
2) v 벡터의 coef sum 분석 : binary classification 같은 문제에서의 feature interaction 영향력을 볼 수 있다.
3) v 벡터의 coef absolute sum 분석 : 절대값의 관점으로 feature interaction 영향력을 볼 수 있다.
'Recommender System > 추천 시스템' 카테고리의 다른 글
| [Recommender System] - 추천시스템과 MAB (Multi-Armed Bandits) (0) | 2021.01.28 |
|---|---|
| [Recommender System] - 임베딩 벡터의 Nearest Neighbor를 찾는 과정 (0) | 2020.12.03 |
| Microsoft Research Learning to Rank 알고리즘 - [1] RankNet (2) | 2019.10.31 |
| Learning to Rank와 nDCG (0) | 2019.08.13 |
| [Recommender System] - 개인화 추천 시스템의 최신 동향 (7) | 2019.06.17 |



