이번 글에서는 검색/추천 시스템에서 가장 중요한 문제 중 하나인 Vector Space 안에서의 Nearest Neighbor를 찾는 문제에 대해 이야기하려고 한다. 이 문제가 중요한 이유는, ML을 활용하여 검색이나 추천에 활용되는 Item을 Densed Vector로 표현하는 것이 가장 보편적인 방법이 되었기 때문이다. 대표적인 예는 Collaborative Filtering에서 사용되는 Latent Factor이며, 최근에는 Word2Vec과 같이 자연어 처리에서 힌트를 얻은 임베딩 방법을 더 많이 사용하는 듯 하다.
개인적으로 최근에 Densed Vector의 Similarity를 real-time으로 줄세우는 작업을 많이 하게 되었는데, 이러한 Vector Search를 빠르게 구현하기 위해 intuitive한 내용들을 개인적으로 정리할 필요가 있었다. 그래서 이 글은 Nearest Neighbor를 찾는 방법과 그 동작 원리에 대해서 Intuitive하게 정리한 개인 메모를 블로그에 옮긴 것에 지나지 않는다. (허접한 내용이니 알아서 도망치라는 이야기)

먼저 가장 간단한 추천 서비스의 시나리오를 가정한다. 현재 보고 있는 영화와 가장 유사한 영화를 추천해주는 것이 우리의 과제라고 하자. 그리고 이미 모든 영화는 100차원의 벡터로 표현되어 있다. 그렇다면 우리가 추천해줄 수 있는 Item의 후보는 100차원으로 표현된 수 백만 혹은 수 천만개의 아이템이 될 것이다. 바로 이러한 상황에서 Item vector 간에 유사도를 계산하는 문제를 풀어야 한다.
하지만 유사도 계산은 엄청난 계산 비용이 들어가게 되고 더 큰 문제는 이걸 실시간으로 계산해야한다는 것이다. 그래서 Brute Force 방법으로는 이 문제를 풀 수 없으며, 대신에 k-Nearest Neighbor를 찾기 위한 별도의 벡터 색인 작업이 필요하다. 벡터를 색인한다는 것은 유사 벡터를 빠르게 찾을 수 있는 데이터 구조를 구축하는 것을 의미하며, 해싱 기반의 방법, 트리 기반의 방법, 네트워크 기반의 방법 등 여러가지 방법이 있다. 이런 방법들은 Brute Force만큼 정확하지는 않겠지만, 대략적으로 빠르게 찾는다는 의미에서 ANNS(Approximated nearest neighbor search)라고 불린다. 이제 몇 가지 방법들의 핵심 아이디어만 intuitive하게 알아보자.

1) 해싱 기반의 접근법
가장 많이 사용되는 방법은 해싱 기반의 방법이다. 이 방법은 Elasticsearch 같은 검색 엔진(7 버전 이상에서 제공하는 densed vector similarity 기능), 혹은 Annoy같은 라이브러리에서 주로 사용되는 방법이다. 해싱 방법에는 LSH, PCA 해싱 등 여러 가지 방법이 있지만 원리만 이해하기 위해 역색인을 활용하는 아래의 예제를 알아보자.
만약 [x1, x2, x3, x4...] 으로 이루어진 벡터의 각 요소를 x1 mod M 같은 아주 간단한 해싱 알고리즘으로 매핑했다고 가정하자(해싱 테이블의 크기는 M). 그러면 xn 요소는 임의의 해시값으로 매핑이 되었을 것이고, [a, b, a, c..] 와 같은 결과가 되었을 것이다(a,b,c...M). 이제 역색인 구조로 이것을 다시 살펴본다면, a라는 해싱값을 가지고 있는 벡터 리스트 [v1, v2..], b라는 해싱값을 가지고 있는 벡터 리스트 [v2, v4..]와 같은 인덱스 형태가 될 것이다. 이 구조를 활용하면 유사한 벡터들의 subset을 줄여나가는 방식으로 효율적인 kNN 검색을 할 수 있게 된다.
또 하나의 예로 Annoy 같은 라이브러리에서 사용되는 Random Projection 기반의 알고리즘을 살펴보자. Random Projection은 고차원 벡터를 저차원 벡터로 매핑하는 차원 축소의 개념이다. PCA 혹은 t-SNE 같은 대표적인 벡터 축소 방식과 개념 자체(원래의 행렬을 재현할 수 있는 Middle Factor가 존재한다는 개념)는 거의 유사하다. 단, Random Projection은 Johnson-Linderstrauss Lemma의 수식을 이용하여 N차원이면서 k개의 Point를 가지고있는 벡터를 특정 차원 M으로 매핑해주는 함수를 알고 있다는 것이 다르다. 자세한 내용은 링크의 블로그에서 훌륭하게 설명되어 있으니 참고하자. 어쨌든 이러한 차원 축소 방법을 이용해서, 벡터를 Bucketizing 한 뒤에 이를 Search Space로 활용한다. 이때, 원래의 벡터를 특정한 Space로 편입시키는 과정을 Locality Sensitve Hashing이라고 한다.
2) 트리 기반의 접근법
트리 기반의 접근법은 divide and conquer 아이디어에서 떠올린 것이라고 할 수 있다. 어떻게든 트리 형태로 vector point를 배치하여, O(log n) 시간 안에 인접한 벡터를 찾겠다는 목표를 가지고 만들어진 형태이다. 하지만 아마도 짐작할 수 있듯이, 모든 데이터를 트리에 넣어야 하므로 상대적으로 많은 메모리를 사용하게 된다. 또한 divide 성능에 따라 search의 성능이 매우 크게 좌우될 수 있다는 단점도 있다.
이에 대한 한 가지 예로 트리 기반의 ANNS중 가장 대표적인 kd-tree(K-Dimension Tree)를 간단히 살펴보자. kd-tree는 간단하게는 binary search tree를 다차원 공간으로 확장한 것이라고 할 수 있다. 다만 다른 점은 트리의 레벨 차원을 번갈아가며 비교한다는 것이다.
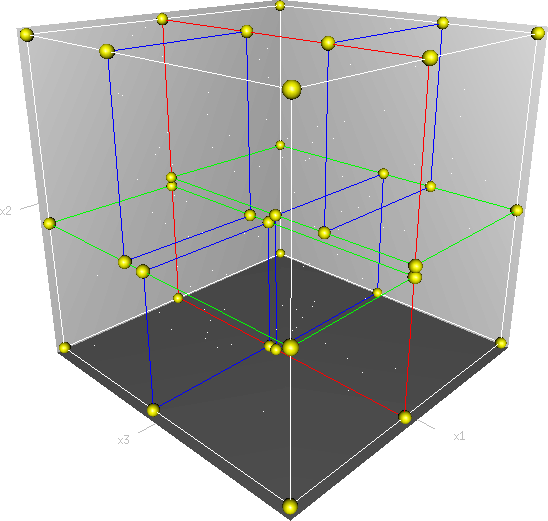
예를 들어 3개의 축을 가진 데이터라고 하면, 위의 그림처럼 하나의 축으로 부피를 분할하고, 나머지 두개의 축 레벨에서 부피를 분할하는 식으로 반복 분할한다. 먼저 X축을 기준으로 YZ 평면을 분할하고, 다음으로 Y축을 기준으로 XZ 평면을 분할, 그리고 Z축을 기준으로 XY 평면을 분할하는 식이라고 이해하면 좋다. 일반적인 BST의 프랙탈 버전이라고 할 수 있겠다.
여기까지 읽으면 이제 Vector Search를 간단히 요약할 수 있게 된다.
1. Vector Search는 point가 매우 많아지면 곤란한 상황이 된다.
2. 그래서 Approximated 계산이 필요해진다.
3. 기본적인 아이디어는 벡터를 공간상에 분리하거나, 해싱 트릭으로 Bucketizing 하는 것이다. 어쨌든 데이터를 큰 그룹으로 나눠놓는 게 목표가 된다.
4. 결국 특정 벡터와 가까운 벡터를 찾으려면, 그룹 내 벡터들과의 거리만 계산하면 된다.
5. 이걸 Real-time으로 활용하기 위해 색인 과정까지 거치면 된다. 검색이니까 역색인을 활용하면 더 좋다. 비유하자면 학생들한테 "너랑 가장 친한 친구가 누구인지 물어볼테니까 미리 결정해놔" 같은 작업이다.
6. Happy Searching!
'Recommender System > 추천 시스템' 카테고리의 다른 글
| [Recommender System] - 결과 정렬에서의 Shuffle 알고리즘 (0) | 2021.04.05 |
|---|---|
| [Recommender System] - 추천시스템과 MAB (Multi-Armed Bandits) (0) | 2021.01.28 |
| [Recommender System] - Factorization Machine (From Scratch with Python) (0) | 2020.04.17 |
| Microsoft Research Learning to Rank 알고리즘 - [1] RankNet (2) | 2019.10.31 |
| Learning to Rank와 nDCG (0) | 2019.08.13 |



